[A18] 利用 SageMath 工具解决一个四次 Diophantus 方程问题

$\quad$ 本文考虑如下问题：若钝角三角形三边长为互素的整数, 且其中一边的边长与这条边上的高的长度之比为 $3:10,$ 求的这条边长度的可能值.
$\quad$ 这实际上是一个求解 Diophantus 方程的问题. 考虑钝角三角形 $ABC,$ 记 $a, b, c$ 为它的三边长. 不妨设 $C$ 为钝角, $BC$ 与 $BC$ 边上的高的长度之比为 $3:10.$ 那么 $a<b<c$ , $a^2+b^2<c^2$ , $BC$ 边上的高可表示为 $\dfrac{10}{3}a.$ 我们的目的是求出互素的正整数 $a,b,c$ 的可能组合. 首先由三角形面积的 Heron 公式有 $\sqrt{s(s-a)(s-b)(s-c)} = \dfrac{5}{3}a^2,$ 这里 $s=\dfrac{a+b+c}{2}.$ 进一步整理便有 $(a+b+c)(b+c-a)(c+a-b)(a+b-c) = \left((c+b)^2-a^2\right)\left(a^2-(c-b)^2\right)=\dfrac{400}{9}a^4.$ 作代换 $X=\dfrac{c+b}{a}, Y=\dfrac{c-b}{a},$ 上式可化为如下的四次 Diophantus 方程 $9(X^2-1)(1-Y^2)=400.$ 我们需要找到这个方程满足 $0<Y<1<X$ 与 $XY>1$ 的有理数解. 注意, 若 $(X_1,Y_1)$ 是此方程的解，则 $(\pm X_1, \pm Y_1)$ 与 $(\pm Y_1, \pm X_1)$ 均是此方程的解. 因此问题转化为在这个方程的曲线上寻找有理点 $(X_1, Y_1).$ 找到这样的有理点后, 由 $X=\max\{|X_1|,|Y_1|\}, \quad Y=\min\{|X_1|,|Y_1|\}$ 便得到了满足 $0<Y<1<X$ 的有理数解，此后再单独判断是否有 $XY>1$ 即可. 为了求解这个方程，首先通过变量代换消去交叉项. 由方程解出 $Y^2 = \frac{9X^2-409}{9(X^2-1)},$ 两边同乘 $9^2(X^2-1)^2$ 便得到 $(9Y(X^2-1))^2 = 9(9X^2-409)(X^2-1)=(3X)^4-418(3X)^2+3681.$ 现在作双有理代换 $X=\dfrac{u}{3}, \quad Y=\dfrac{v}{9(X^2-1)},$ 可将上式化为 $v^2 =u^4-418u^2+3681.$ 我们将问题转化成了寻找这条四次曲线上的有理点对 $(u,v).$ 一般地，对于四次曲线 $v^2 =u^4+ku^2+l (k,l \in \mathbb{Z}),$ 可通过双有理代换 $u=\dfrac{y}{6(x-6k)}, \quad v=\pm\dfrac{18u^2+3k-x}{18},$ 将其化为 Weierstrass 形式： $y^2=x^3-27(k^2+12l)x+54(k^3-36kl),$ 它的判别式为 $\Delta=4\left(-27(k^2+12l)\right)^3+27\left(54(k^3-36kl)\right)^2=-8503056(k^2-4l)^2l.$ 对于本文中的问题, $k=-418, l=3681,$ 可求出 $\Delta=-801273577881600000000 \ne 0,$ 这说明可通过双有理代换 $u=\dfrac{y}{6x-15048}, \quad v=\pm\dfrac{18u^2-1254-x}{18}$ 将四次曲线 $v^2 =u^4-418u^2+3681$ 化为 $\mathbb{Q}$ 上的椭圆曲线 $y^2=x^3-5910192x-952718976.$ 接下来我们只需在这条椭圆曲线上寻找符合条件的有理点. 根据 Mordell-Weil 定理, 一般的椭圆曲线 $E(\mathbb{Q})$ 是有限生成的 Abel 群. 具体地，存在 $r \in \mathbb{Z}_{\geq 0}$ 使得 $E(\mathbb{Q}) \simeq \mathbb{Z}^r \oplus E(\mathbb{Q})_{\mathrm{tors}},$ 这里 $r$ 为 $E$ 的秩, $E(\mathbb{Q})_{\mathrm{tors}}$ 为 $E$ 的挠群，它们是椭圆曲线的基本不变量，可以利用 SageMath 进行求解. 本文中需要考虑的这条椭圆曲线的秩为 $1,$ 其挠群同构于 $\mathbb{Z} / 4\mathbb{Z},$ 因此这条曲线存在分解 $\mathbb{Z} \oplus \mathbb{Z} / 4\mathbb{Z}.$ 进一步还可以计算出其挠群中的四个元素分别为 $(-1092, 64800),$ $(-1092, - 64800),(2508, 0)$ 以及无穷远点，其自由部分的生成元为 $(-372,34560),$ 由它通过自加运算可以生成全部的无穷多个有理点. 完整代码及示意图如下：

from sage.all import EllipticCurve

# 定义椭圆曲线
E = EllipticCurve([0, 0, 0, -5910192, -952718976])
print("椭圆曲线 E =", E)

# 计算基本不变量
print("E 的秩 =", E.rank())
print("自由部分的生成元：")
for P in E.gens():
    print(P)

T = E.torsion_subgroup()
print("E 的挠群部分为：", T)
print("挠群部分的生成元：")
for Q in T.gens():
    print(Q)

# 定义变换函数：输入椭圆曲线上一个非无穷远点，返回 (X, Y)
def transform_point(point):
    if point.is_zero():
        print(f"{n}P = {point} 为无穷远点")
        return None
    x, y = point.xy()
    # 计算 u = y/(6x - 15048)
    denom = 6*x - 15048
    if denom == 0:
        print(f"{n}P = {point} 为挠点")
        return None
    u = y / denom
    # X = u/3
    X_val = u / 3
    # 计算 v = (18u^2 -1254 - x) / 18
    v = (18*u*u - 1254 - x) / 18
    # 若 X^2-1 为 0 则无法定义 Y
    if X_val**2 - 1 == 0:
        print(f"{n}P = {point} 为挠点")
        return None
    # 利用 v^2 = (9Y(X^2-1))^2 得 Y = v/(9*(X^2-1))
    Y_val = v / (9 * (X_val**2 - 1))
    
    # 留下 X > 1, 0 < Y < 1 的解
    if abs(X_val) > abs(Y_val):
        X_val = abs(X_val)
        Y_val = abs(Y_val)
    else:
        X_val, Y_val = abs(Y_val), abs(X_val)
    
    return (X_val, Y_val)


# 考察 nP, n 从 1 到 8（可根据需要扩大范围）
valid_points = []
P = E(-372, 34560) # 生成元 (-372, 34560)
for n in range(1, 8):
    Pn = n * P
    if Pn.is_zero():
        print(f"{n}P = {Pn} 为无穷远点")
        continue
    trans = transform_point(Pn)
    if trans is None:
        continue
    X_val, Y_val = trans
    # 检查约束条件 XY > 1
    if  X_val * Y_val > 1:
        valid_points.append((n, Pn, X_val, Y_val))

# 输出满足条件的点及其对应的 X, Y
if valid_points:
    print("\n满足约束条件的有理点及其变换后的 (X, Y):")
    for n, Pn, X_val, Y_val in valid_points:
        print(f"{n}P = {Pn}  ->  X = {X_val}, Y = {Y_val}")
else:
    print("\n没有找到满足约束条件的有理点。")

from sage.all import EllipticCurve

# 定义椭圆曲线

E = EllipticCurve([0, 0, 0, -5910192, -952718976])

print("椭圆曲线 E =", E)

# 计算基本不变量

print("E 的秩 =", E.rank())

print("自由部分的生成元：")

for P in E.gens():

print(P)

T = E.torsion_subgroup()

print("E 的挠群部分为：", T)

print("挠群部分的生成元：")

for Q in T.gens():

print(Q)

# 定义变换函数：输入椭圆曲线上一个非无穷远点，返回 (X, Y)

def transform_point(point):

if point.is_zero():

print(f"{n}P = {point} 为无穷远点")

return None

x, y = point.xy()

# 计算 u = y/(6x - 15048)

denom = 6*x - 15048

if denom == 0:

print(f"{n}P = {point} 为挠点")

return None

u = y / denom

# X = u/3

X_val = u / 3

# 计算 v = (18u^2 -1254 - x) / 18

v = (18*u*u - 1254 - x) / 18

# 若 X^2-1 为 0 则无法定义 Y

if X_val**2 - 1 == 0:

print(f"{n}P = {point} 为挠点")

return None

# 利用 v^2 = (9Y(X^2-1))^2 得 Y = v/(9*(X^2-1))

Y_val = v / (9 * (X_val**2 - 1))

# 留下 X > 1, 0 < Y < 1 的解

if abs(X_val) > abs(Y_val):

X_val = abs(X_val)

Y_val = abs(Y_val)

else:

X_val, Y_val = abs(Y_val), abs(X_val)

return (X_val, Y_val)

# 考察 nP, n 从 1 到 8（可根据需要扩大范围）

valid_points = []

P = E(-372, 34560) # 生成元 (-372, 34560)

for n in range(1, 8):

Pn = n * P

if Pn.is_zero():

print(f"{n}P = {Pn} 为无穷远点")

continue

trans = transform_point(Pn)

if trans is None:

continue

X_val, Y_val = trans

# 检查约束条件 XY > 1

if X_val * Y_val > 1:

valid_points.append((n, Pn, X_val, Y_val))

# 输出满足条件的点及其对应的 X, Y

if valid_points:

print("\n满足约束条件的有理点及其变换后的 (X, Y):")

for n, Pn, X_val, Y_val in valid_points:

print(f"{n}P = {Pn} -> X = {X_val}, Y = {Y_val}")

else:

print("\n没有找到满足约束条件的有理点。")

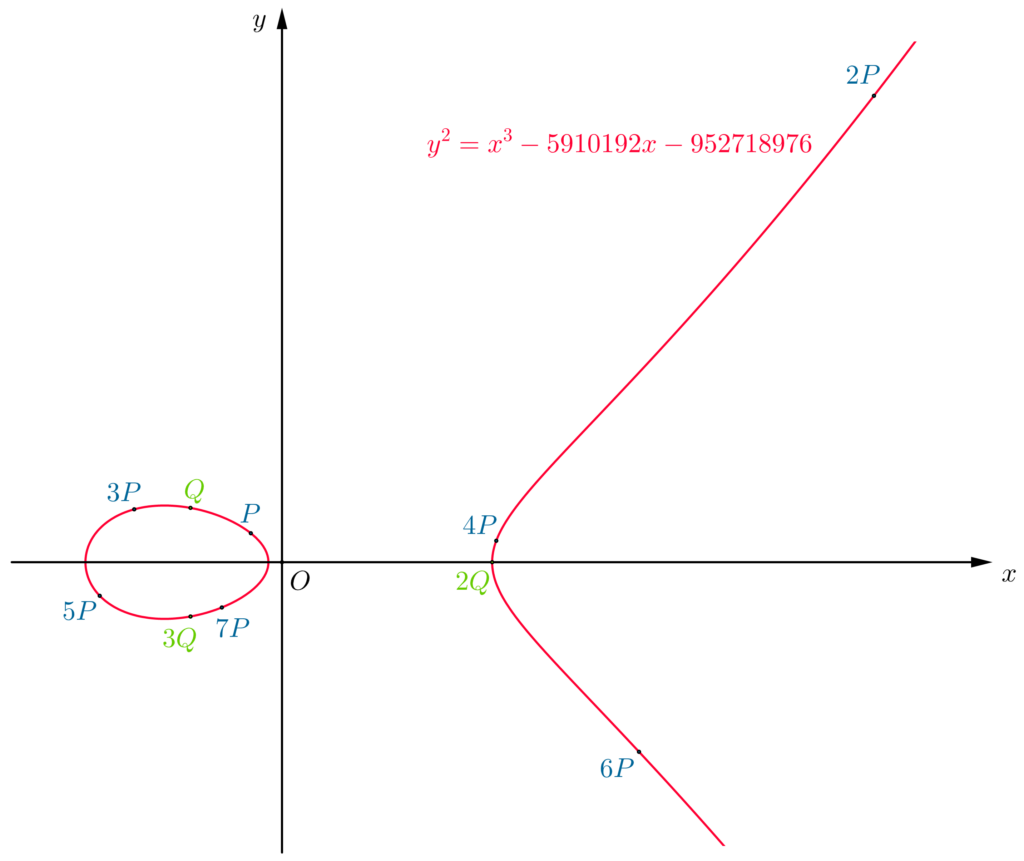
$\quad$ 经计算, 前七个有理点为： $\begin{aligned} & P=(-372,34560), \\ & 2P=\left(\dfrac{28257}{4},\dfrac{4452975}{8}\right), \\ & 3P=\left(-\dfrac{770514132}{436921},\dfrac{18232500384000}{288804781}\right), \\ & 4P=\left(\dfrac{197840637553}{77369616},\dfrac{17408865486415625}{680543142336}\right), \\ & 5P=\left(-\dfrac{10229587945765554612}{4701773724609361},-\dfrac{12924696291376974306172704000}{322398184075900811511641}\right),\\ & 6P=\left(\dfrac{3315857515978138943646417}{778265695724123543524},-\dfrac{4913082978666096182700219050478483225}{21711600145951982612977114447768}\right),\\ & 7P=\left(-\dfrac{980310927987768717199615170184212}{1365254122130421423237129886921},-\dfrac{86213265029332223182933554501882177755794614946560}{1595218746624712341752806736238641171325979781}\right),\end{aligned}$ 其中 $P,3P,4P,5P,6P,7P$ 对应于曲线 $9(X^2-1)(1-Y^2)=400$ 上的点 $(X,Y)$ 满足 $XY>1$ , 分别为 $\begin{aligned}&(X, Y) = \left(9, \dfrac{2}{3}\right), \\ &(X, Y) = \left(\dfrac{955341}{81499}, \dfrac{262142}{319263}\right), \\ &(X, Y) = \left(\dfrac{11299872121}{390278520}, \dfrac{10989319079}{11293130329}\right), \\ &(X, Y) = \left(\dfrac{10818894959910981}{1415347510692259}, \dfrac{1710716537700542}{3597581681140263}\right), \\ &(X, Y) = \left(\dfrac{93484504350405221240653}{13032444705716745260028}, \dfrac{6390174904465811823103}{18514327358706141569665}\right),\\ &(X, Y) = \left(\dfrac{12943448758278309403238895165969}{709092463025904829132403703241}, \dfrac{4034454167364911033269090973762}{4334844983868375725354843829243}\right),\end{aligned}$ 对应的三角形边长的第一组值为 $a=6, \quad b=25, \quad c=29,$ 第二组值为 $\begin{aligned}& a = 52039230474, \\ & b = 283640722825, \\ & c = 326369344541, \end{aligned}$ 第三组值为 $\begin{aligned}& a = 8814932381938466160, \\ & b = 123322033377526774729, \\ & c = 131899823749446540889, \end{aligned}$ 第四组值为 $\begin{aligned}& a = 10183656553827886989599214648234, \\ & b = 36500599924821923135078595423625, \\ & c = 41343116711091007465123514432381, \end{aligned}$ 第五组值为 $\begin{aligned}& a = 482573895131753093455040731485630241003701240, \\ & b = 1647523115407481222922163366417259231656764361, \\ & c = 1814082317612100178364265041163661384602418129, \end{aligned}$ 第六组值为 $\begin{aligned}& a = 6147611812893430459047690640742368681943631952471980499353126, \\ & b = 53247042881278175108210271527885380230155873953848266415268825, \\ & c = 58968644966281996768619784995061807221900024946019897545994109.\end{aligned}$ 更多的取值组合可由上述方法依次求出.

发表评论 取消回复

发表评论取消回复